INTRODUCTION

With the publication of Large Language Models (LLMs), students are tempted to solve their school problems by using AIs such as ChatGPT, Bard, etc. However, recent studies show that LLMs cannot solve physics problems well (Gregorcic and Pendrill 2023). Indeed, LLMs are neural models that try to predict the next word of the answer probabilistically. Thus, neither students nor engineers can trust the output of the model.

Solving word problems is a classic and challenging field of AI programming. The automatic solving of such problems involves natural language processing, a well-formed problem representation, and a good problem-solving strategy.

In this paper, we want to study the automatic solving of physics word problems.

There are several reasons for the relevance of our paper:

• The field of word problem solving is very diverse, and its research has not developed as quickly as the research, for example, of neural networks.

• A significant research gap exists in understanding how to solve word problems within specific scientific fields (such as physics, chemistry, etc.) , whereas MWP solving has been a well-established area of study.

• Physics word problems bring new challenges in automatic solving that require specific techniques to overcome them.

• While many arithmetic word problem data sets exist, there is no widely used collection of physics problems.

We want to revive the classic AI approach where programs solve human problems in a correct and deterministic way, where programs utilize the field knowledge, rules, and definitions to give a strict and accurate answer.

LITERATURE ANALYSIS

STUDENT: Pioneer AI program

The D. Bobrow’s STUDENT program is one of the first AI programs to understand natural language, showing promising results (Bobrow 1964). The program solves algebraic word problems stated in English. An example of the problem that STUDENT can handle:

“If the number of customers Tom gets is twice the square of 20% of the number of advertisements he runs, and the number of advertisements is 45, then what is the number of customers Tom gets?””

The STUDENT approach is straightforward: the problem is represented as a set of simultaneous equations; the solution of the problem is the solution for that set. The program used pattern matching and kernel sentence theory to transform English text into a set of equations. For the example above, STUDENT would generate this system:

$$\{\begin{array}{l}(CUSTOMERS)=2\ast (0.2+(ADVERTISMENTS){)}^2\\ (ADVERTISMENTS)=45\\ ?=(CUSTOMERS)\end{array}$$

Words in the problem text resemble mathematical operations and variables, so the STUDENT can translate the English text into mathematical expressions using pattern matching. The question mark is a special symbol used to denote the unknown value. The variables in the equation are subparts of the problem text.

When the set of equations is unsolvable, the STUDENT will try to solve it again with several techniques applied. For example, STUDENT may change variable names to be equal if they have some words in common (e.g., “SPEED” and “SPEED OF THE CAR”). Or, the STUDENT may add new equations from its internal knowledge of the world.

The STUDENT program is nearly 60 years old. The field of AI programming has improved since that time. Peter Norvig presented an analysis and elegant implementation of STUDENT written in Common Lisp in functional programming style (Norvig 1991).

Math word problem solvers

We want to continue the literature overview by analyzing math word problem solvers. We want to inherit the researched knowledge of natural language processing and problem representation that is studied in this field of word problem-solving.

Here is the list and analysis of different problem representations for MWPs structured by Mandal et al. (Mandal and Naskar 2019):

• Equation template representation. An equation template is a predetermined equation that is formed with arithmetic operations and with two types of unknowns (called slots): unknown variables and numbers. Using statistical approaches, the words in the problem are aligned into these unknown slots.

• Equation tree representation. The whole problem is converted into an equation tree using statistical methods. Usually, recognizers generate several trees, so another approach is applied to choose the best.

• Entity and state transition-based representation. In this approach, the problem consists of states and state transitions. A state contains all the information of the known objects (their owners, count, and type). State transition would change the count of belonging objects, which can result in an equation.

• Tag-based representation. In this method, the text is processed in several stages. First, it is tokenized and parsed. Then, the type of problem is recognized. After that, several logic forms representing grammatical relations and quantities are generated. An answer is generated using special techniques.

The natural language processing of MWPs has many methods, including rule-based techniques and statistical and neural models. Often, solvers parse the English text into dependency trees. Common features extracted from the text are part of speech tag, the lemma of a word, quantities, units of quantities, comparative adverbs, dependencies between verbs and quantities, etc. (Zhang et al. 2020).

Physics word problem solvers

There is not so much research and categorization on PWP solvers. Most programs date back to 1970-1980 and use their own knowledge representation and custom natural language processing methods.

One of the first programs that could handle PWP is the NEWTON program by Kleer (Kleer 1977). It is made to solve mechanical problems. NEWTON would analyze the programs text and convert it to several data structures. The first data structure depicts objects, and the second is a tree-like data structure (called “envisioning tree”) that holds all possible states of the objects. The trees root is the starting position, and the next children are the next events. When the tree divides, it means that there are several possibilities where an object could move. Quantitative knowledge is presented in a data structure called FRAME. It stores all the known parameters of the object and the equations that connect those parameters.

Gordon S. Novak Jr. has studied the topic of physics problems very thoroughly. One of the programs he developed is ISAAC (Novak 1976). This problem understands and solves physics problems that involve rigid bodies in static equilibrium. The program can also draw a diagram of the problem.

ISAAC problem analysis consists of lots of stages, and they have several branches. Firstly, an augmented transition network transforms the English text into structured parsed sentences. Then, the semantic analysis is performed. It is used to determine the meaning of verbs and prepositions. After several stages, a canonical object model is formed. In this data structure, objects in the problem are represented as physics objects (point, pivot, lever, etc.). The canonical object model is then passed to the EUCLID program, which analyzes the orientation of objects and assigns coordinates to them. After that, the geometric model is formed. Problem-solving involves creating a set of equations that represent physical laws between objects.

The ISAAC program is big and complex. It is hard to analyze it because of its age and programming style. As the author states, 44 pages of Lisp code is written only for parsing the English text, while problem-solving is one of the simplest parts of the program. We were unable to find the source code of the ISAAC program.

Bundy et al. created the MECHO program, which addresses mechanical PWPs and is implemented in Prolog (Bundy et al. 1979). The program processes the word problem in several stages. First, it parses the text, extracting information. Then, MECHO derives assertions related to objects, given parameters, and unknown values from the parsed data. These assertions are then transformed into a particular data structure called schema, where inference rules, resembling logical representations of physics laws in Prolog, are applied. MECHO can provide either symbolic or numerical solutions.

Mukherjee et al. have an extensive overview of rule-based word problem solvers and a dedicated section for PWPs. Other programs for solving PWPs include BEATRIX, ALBERT, and FREEBODY (Mukherjee and Garain 2008). All those programs address only specific types of physics problems. As the reader may notice, all the names of the programs resemble human names and are written in upper-case. Possibly, this tradition came after the STUDENT program.

We have found a modern paper on PWP solving. Leszczynski et al. address the problems of a free-falling object under constant acceleration of gravity (Leszczynski and Moreira 2017). The problem is analyzed using several recurrent neural networks (RNN), then the dynamical system is formed, and the solution is provided at the end. The first RNN is a word labeler used to extract the given values and the problem question. The second RNN is a classifier that determines the type of question. While this work seems modern and interesting, the accepted problem set is limited and generated artificially using context-free grammar.

Conclusions of literature analysis

We have investigated the design of several word problem solvers. Unfortunately, we concluded that a few techniques apply to make a generic PWP solver. Or at least the known methods cannot solve problems from Ukrainian physics textbooks.

There are some issues in using STUDENT to solve physics problems. Consider the problem: “If the distance between Dnipro and Kyiv is 477 kilometers and the time the automobile has traveled is 6 hours, then what is the speed of the automobile?”. The STUDENT would generate this set of equations:

$$\{\begin{array}{l}(DISTANCE)=477kilometers\\ (TIME)=6hours\\ ?=(SPEED)\end{array}$$

As the reader may notice, the STUDENT has generated a system consisting of given values and unknowns. This set would resemble the column “Given”, which is usually written by students. But the physics problem cannot be represented like this set of equations for two reasons:

1. This set is unsolvable. A set of equations requires that all the information needed to find the unknowns is present in the set. But our example has no connection between speed, time, and distance.

2. There is a theoretical issue. In math, variables represent unknown values and act like bound variables in lambda calculus: their names can be changed freely unless they interfere with another name. But in the physics field, the name of variables has a special meaning. It is a given value that marks some parameter of an object.

In this example, STUDENT would add needed equations from its internal knowledge using the search on the first word of a variable (it may find the relation “the distance is equal to time multiplied by speed ”). While this approach may work for simple problems like the one above, it is not the best solution because it is too chaotic and brute-force-like.

The approaches presented in subsection 2.2 are not sufficient to represent physics problems. They are constructed around math expressions, though in PWP, usually there are no explicitly stated expressions (only given values are specified).

Most papers for word problem-solving are outdated. They use unstandardized programming languages with undefined styles of programming. The analysis of the capabilities and limitations of previous works is not enough.

OBJECT, SUBJECT, AND METHODS OF RESEARCH

Object and subject

The object of our research is automatic word problem-solving. The subject of our research is the automatic solving of physics word problems.

Method of the research

To study the subject, we developed a program that can solve basic PWPs stated in the English language, which do not involve any dynamic change or complex representation. Also, we do not support solving problems where a graphical model is needed (forces, impulses, energy, etc.).

The whole program was written in Python language. We have separated our program into two projects: one is a user interface, and the other is the core library. The technology stack of the user interface consists of Django (web framework), MathJax (LATEX output), and Bootstrap (graphical design). The library uses spaCy (natural language processing) and SymPy (symbolic math) libraries. We used PythonAnywhere to host our program ( https://inanyan.pythonanywhere.com/).

By definitions provided in AI:MA (Russell and Norvig 2009), we consider our program to be inside the “Thinking Rationally” field because we are trying to find the computational model behind PWP solving and provide the user with a correct problem solution.

The whole NLP pipeline, algorithms, and data structures that are used by our program can be depicted through this diagram:

In fig. 1 nodes represent algorithms, right after the node comes a brief comment on the chosen approach, and the labels of the arrows are data structures. In section IV of the paper, we will describe all the steps of the program, but before that, we will discuss the found types of physics problems to understand what features we need to extract from English text.

Testing data

To test our program, we created a small dataset with physics problems collected from various sources such as (Гельфгат 2009), (Ненашев 2011), and the Internet. We translated the Ukrainian variants to English.

DESCRIPTION OF THE PROGRAM

Problem types

The first thing we did before starting to make this program was to study available PWP. We noticed that PWPs fall into five categories:

• Theoretical problem: “Why do we not observe the daily rotation of the earth in everyday life?”.

• Value conversion problem: “The car is traveling at a speed of 108 kilometers per hour. Represent this speed in meters per second”.

• Value comparison problem: “Which speed is bigger: 10 meters per second or 10 kilometers per hour?”.

• Unknowns finding problem: “The car drove for 40 minutes at a speed of 144 kilometers per hour. How far did the car travel?”.

• Calculation of the change of a value depending on other value changes: “How many times will the speed of wave propagation increase if the wavelength increases by three times and the period of oscillation remains unchanged?”.

We decided not to solve the theoretical problems because they require an extensive ontology of physics definitions and laws, while we were more focused on computational problems.

Named Entity Recognition

We chose the named entity recognition (NER) method for the feature extraction task. In this method, subparts of text, called entities, are marked with a particular string that represents the type of an entity.

We have collected the information about which entities our program should recognize:

• Given values: “the distance is 10 kilometers”, “the mass is 50 grams”, etc.

• Unknown values: “What is the speed…”, “Determine the density of…”, etc.

• Units: “meters per second”, “kilogram”, “Newton”, etc.

• Value changes: “time is increased by a factor of 2”, etc.

For NER, we chose a rule-based method – pattern matching. We will present the patterns we used for NER with our modified BNF notation because there is no standardized way to do this. In this notation, no recursion is allowed. Terminals are written as is and may resemble either the lowercase form of a token or its lemma. Non-terminals are written inside ‘<’ and ‘>’. Entities are written as non-terminals whose names are written in uppercase form; the other non-terminals are fragments used only for easier construction of the grammar. The special rule <like_num> denotes one token resembling a number. An ellipsis indicates a part of the rule that was shortened in the paper.

Here is the list of all the rules:

We provide here an example of NER to understand this process better:

Problem type recognition

The program determines the type of problem by looking at the presence of entities. The algorithm can be described in English like this:

1. If there is a CHANGE_VERB entity, then it is a value change problem.

2. If there is a UNIT entity, then it is a conversion problem.

3. If there is a COMPARSON_WORD entity, then it is a comparison problem.

4. If there is an UNKNOWN_QUESTION or UNKNOWN_HOW_QUESTION entity, then it is an unknown finding problem.

5. Otherwise, the program cannot recognize the type of problem.

Entities to problem representation conversion

The algorithm for converting a list of entities to problem representation according to the recognized problem type can be described like this:

1. For value conversion problem, extract a quantity and a unit.

2. For value comparison problems, extract two quantities.

3. For unknowns finding problem, extract given and unknown values.

4. For value change problems, extract the value changes and the value in question.

To convert a quantity into the internal math representation, the program converts the number (the first token) and the unit (the rest).

We have found that units in SymPy are written as regular English words, allowing us to use Python’s insecure “eval” function. The program will convert the unit entity into a valid Python expression and call the “eval” function. We replace the word “per” with the division symbol. To parse the modifiers “square” and “cube”, we replace those words with “**2” and “**3”, respectively, after the single unit.

We have found two ways in which given values are encoded in the list of entities. It is either a pair of TERM and QUANTITY or a single QUANTITY.

To convert the pair of TERM and QUANTITY into a given value, the program needs to convert the term into a symbol (the QUANTITY will be the value of a given variable). The program uses a hard-coded map data structure, the key to which is a string, and the value is a symbol (e.g., “force” is F , “mass” is m , etc.).

A special technique for determining the symbol should be applied to convert a single QUANTITY into a given value. We have found that looking at the unit of a quantity can infer the variable. If the unit is one English word, the program uses a hard-coded map data structure (e.g., “meters” is S , “seconds” is t , etc.).

The conversion of compound units and units with modifiers is tricky. However, we noticed that compound units resemble a physical formula (e.g., “meters per second” corresponds to $v=\frac{S}{t}$, etc.). So, the program will first convert all one-word units in the compound unit to the symbols. Then, if the expression is not a single unit, the program will search the list of formulas for a formula, the right-hand side of which is identical to the result expression.

The whole process described above ended up being so powerful that the program will use it while presenting the output of value comparison and conversion problems.

Unknown values are encoded either as a pair of UNKNOWN_QUESTION and TERM or as a single UNKNOWN_HOW_QUESTION. For the first variant, it is sufficient to convert the TERM into a variable, and for the second variant, we use a hard-coded map data structure (e.g., “how far” is S , “how fast” is υ , etc.).

Value changes are encoded as a pair of TERM and POS_CHANGE or TERM and NEG_CHANGE. To convert these pairs into a variable change, the program should infer the variable by the TERM entity and determine the factor of the variable change. According to our NER rules, the factor number comes at the end of the POS_CHANGE and NEG_CHANGE. So, it is enough to parse the last token in the span. If the entity is NEG_CHANGE, the parser should also take the numbers reciprocal.

The value under change is encoded as a pair of TERM and CHANGE_WORD. It is enough to infer the variable from the TERM entity.

Problem-solving

Solving value conversion and comparison problems is trivial, and it is a primitive operation in the SymPy library, so we will not describe these processes. However, we note that for value comparison problems, the program will convert the second value to the unit of the first value.

We define the solution to unknowns finding problems as a list of formulas. This list resembles a plan of actions that the computer should perform. The calculation of the final answer is delegated to the output part of our program.

The first attempt to solve an unknown finding problem would be to use a search algorithm for each unknown variable to find a formula left-hand side of which is equal to the unknown. But this approach is wrong for several reasons:

• The program could find several applicable formulas for one unknown.

• The formula may contain an unknown variable (a variable that is not given). However, it is possible to find another formula that could be used to find those variables.

• One physical formula can be used to find several variables. Consider the second Newton’s law: F = m a . This formula can be used not only to find a force but also a mass (if the force and the acceleration are known) or an acceleration (if the force and the mass are known).

These discussions guided us to make this recursive algorithm:

1. Find an applicable formula for the unknown variable.

2. Create a set difference of given variables and the free symbols in the found formula. This set will resemble the set of unknowns of a formula.

3. If the set is empty, return a list of one element containing the found formula (base case).

4. Otherwise, perform these steps:

   1. For each element in the set, apply this algorithm (recursive step).

   2. Combine all the results. The final result is a list.

   3. Append the found formula to the list.

   4. Return the list.

We described this algorithm informally because the algorithm can fail in several steps. If the algorithm fails on step 1 or step 4.1, this may mean two things: the program cannot find the solution for the unknown variable in the problem representation, or the program should find another formula to apply.

Also, we used the term “applicable formula”. This means the formula belongs to the internal list of formulas or is derived.

We have quickly noticed that this algorithm is a simplified version of the Stanford Research Institute Problem Solver algorithm (Fikes and Nilsson 1971). So, we modified it to the physical field. The goals are represented as math symbols. The operators are the applicable formulas. The preconditions of an operator (or a formula) are the free symbols of the formula. The initial step is represented as a set of given.

We define the solution to a value change problem as an ordered pair of a floating-point number and a formula. The number is the result of dividing the value of a changed value and the original value, and the formula is used to present the output for the user.

We invented this problem-solving algorithm for this problem type:

1. Find a formula for which the given variables are a subset of the formula’s variables.

2. Substitute each formula variable with the given variables as a “factor * variable”.

3. Divide the derived formula with the original formula.

4. If the result is a number, then it is the answer to the problem.

5. Otherwise, repeat from step #1 and find another formula.

The algorithm may fail at step 1 or 5, meaning the program could not find the formula to calculate the change. The algorithm is simple, and it resembles human thinking.

Context

The first time we made a prototype of the program, we noticed it was limited. Consider a problem: “What is the optical power of a converging lens with a focal length of 40 centimeters?”. A special formula solves this problem ($D=\pm \frac{1}{F}$ ). However, the formula varies whether the lens is a converging lens or a diverging lens. Another situation when we find this peculiarity is when we need to calculate the surface of an object (squares, rectangles, triangles, etc.).

We introduce the term context to encode the information about a physical object. Context is a set of strings that encode objects and their qualities. Examples of context words: “lens”, “converging”, “diverging”, “square”, “cube”, “rectangle”, etc. In each physics problem, there is an associated context.

RESULTS

Examples of program usage

We will present the solution of 4 problems with different types and comment on how the program solved them.

Problem #1: “The car is traveling at a speed of 108 kilometers per hour. Represent this speed in meters per second”.

Problem #1 is a conversion problem. We haven’t found many problems of this type. The program correctly recognized the given quantity and target unit. There is no detailed explanation of the solution because conversion is a primitive operation in SymPy.

Problem #2: “Which speed is slower: 72 kilometers per hour or 24 meters per second?”.

Problem #2 is a comparison problem. It is not trivial to compare $72\frac{km}{h}$ and $24\frac{m}{s}$. The program correctly recognized two quantities and the type of the problem. According to our problem-solving strategy, the program converted the second value to the unit of the first value. Also, our program generates answers based on the word that was asked. For example, if the question asks for greater value, the answer will show greater value, and in this example, the program tells us about slower value.

Problem #3: “To raise a marble column weighing 3.78 tons from the bottom of a lake, 95200 joules of work was done. Determine the depth of the lake”.

Problem #3 is an unknown finding problem. We chose this problem because it is not so trivial to solve; it includes several formulas for the solution. Unfortunately, this example shows some peculiarities of SymPy and our implementation, which we will discuss in the following subsection.

The program correctly recognized the given variables and the unknown variable. The program correctly found the solution, including the gravitational force and work formulas. Additionally, the program derived the height from the work formula.

Problem #4: “How many times will the moment of a force change if the force is increased by a factor of 8 and the arm of the force is decreased by a factor of 4?”.

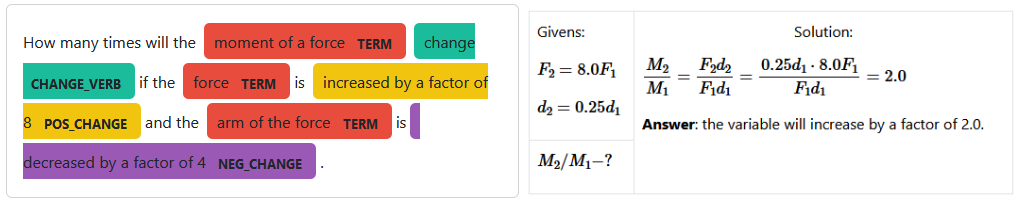
Problem #4 is a value change problem. A parser is needed to convert the list of entities to the problem representation fully. The program correctly recognized the given changes and the value under question. The program found the required formula and performed a substitution, which resulted in a number.

Special attention is required to the term entities. We included the preposition “of” in the term. Usually, while recognizing noun phrases (NP), different NPs stay away, but we combined them and determined the variable based on the first words. If we did not make this decision, an ambiguity would arise: do we need to find the change of the moment or the force?

Analysis of limitations of the program

We performed a thorough analysis of issues that our program has. We grouped the issues into several categories:

1. Complex problem types.

2. Imperfect natural language processing.

3. Inaccurate problem type recognition.

4. Incomplete problem representation.

5. Imperfect problem-solving techniques.

6. Symbol is semantically equal to terms and objects.

7. Issues with libraries that we use.

We want to begin the analysis of the limitations of our program by analyzing our problem-type classification. We have found that our types can have new subtypes. Consider the problem: “Can a wedding ring with a volume of 0.5 cubic centimeters and a mass of 8 grams really be gold? ”. It is a new question type for which the answer is a Boolean value. But it is easy to notice that this is a subtype of unknown finding problem. The program must compare the object’s density to the actual gold density.

There are lots of issues with natural language processing. We have found that the solution to the problem depends highly on the problem formulation. A possible reason is that we used a rule-based approach for NER. Rule-based techniques are usually used on the first iteration of NLP program development, and then they are replaced by more powerful statistical or neural models (B. et al. 2020).

Pattern matching, used for NER, restricts the input text to a specific syntax. For example, we require that the units are written as proper English words instead of their abbreviations. The program cannot recognize numbers that are not written with decimal notation (e.g., “one second”). The patterns require that every quantity has a corresponding unit (the program cannot parse “1 and 4 kilograms” as two quantities). Change of a value should be written as “increased by 9” or “reduced by a factor of 2” (but the program cannot parse “the value is halved” or “doubled ”). There are many ways to formulate the problem, so there could be lots of patterns in the text that the programmer may miss.

Another interesting problem that our application has is that it cannot support tasks with named constants. The program cannot infer that the “length of the equator” is about 4 ⋅ 10⁴ k m . Also consider the problem: “Find the volume of mercury weighing 2 kilograms ”. The program needs to refer to the table of densities and update the problem representation. Our implementation does not do it.

The most interesting issue with parsing English text is that it is easy to deceive the program. Consider the problem: “The airplane flew 1200 kilometers in 2 hours. At what speed did the airplane fly?”. The program can handle it. But if the user adds this sentence to the end of the text: “Represent the result in meters per second ”, then our implementation will think that this problem is a value conversion problem. So, looking at keywords is not the best approach to determine the type of problem.

Our problem representation is too basic. The physics problem is not a set of given variables and unknowns. An image or a diagram may be included, but the program cannot analyze them. An equation may be offered.

However, one of the biggest issues with problem representation is that we do not support several objects in the task. The program cannot recognize the two velocities of two bodies or two capacitors capacitance values in an electric chain. The problem lies in the representation of variables; we use only one symbol for them, but an index could also be used in the real world.

The solution to some problem types may be more complicated than we provide. This can be illustrated by this problem: “ The masses of two steel balls are 1 kilogram and 4 kilograms. Which of the balls has the greater volume? By how many times? ”. Again, it is a simple problem for a human to solve, but not the computer. Our program would think this is a comparison problem and happily answer that 4 kilograms is bigger than 1. The program should use a formula for inferring the volume of objects, but our implementation handles only the given quantities.

Our problem-solving strategy for value change problems is imperfect. We defined that the answer to a value change problem results from division. But we can compare values not only with division but also with subtraction. Also, we implicitly assume that the physical formulas are created with multiplication and division of variables so that the variables will be reduced in the division step. But if the formula is formed with addition, then this strategy will not work.

Consider the problem: “How would the mass of an iron ball change if its radius is increased by a factor of two? ”. This problem requires two formulas to find (one for the volume and one that involves the density of iron). It is easy to notice that we can reuse the STRIPS algorithm to find the unknowns of the first formula, but there lies a new degree of complexity.

We propose a hypothesis that it is impossible to construct an efficient algorithm for solving value change problems. For every unknown variable in the formula, the program should decide whether to leave it as is (hoping it will be reduced in the division) or to find another formula. But that second formula could also have unknown variables. Moreover, it may miss some changes if the program doesn’t use a formula for some unknowns.

There is a theoretical issue with our program. Our problem-solving algorithm treats physical terms and objects as variables. But, in the real world, variables resemble physical terms. With this issue, an ambiguity arises: c may mean either capacitance or speed of light, but the program considers these terms equal because they are written with the same symbol.

We have used a special technique for treating a QUANTITY entity as a given value if there is no TERM entity. If the program encounters a “2 meters”” entity, it will treat it as S = 2 m . We have found that this is another ambiguity in our implementation. This entity can be not only S , but also l , h , d , etc.

There are also various issues with the libraries we use. The SymPy treats the unit of a physical value as a variable, so problems with printing may arise. Another problem is that SymPy does not know that Joule divided by Newton is a meter. Not enough units are provided in the SymPy library. The library documentation is too short, and we have not found a simple way to resolve these issues.

CONCLUSIONS

In this paper, we have studied the automatic solving of physics word problems. PWP solving is a challenging subfield of word problem solving that requires complex problem representation. We have found that researched solutions for math word problems are unsuitable for solving PWP. Current PWP solvers are focused on specific problem types, while we were interested in generic PWP solvers.

To study our papers object and subject, we developed and described a program that could solve simple physics problems. Our testing dataset was formed from Ukrainian physics textbooks. The development of word problem solvers focuses mainly on problem representation, natural language processing, and problem-solving strategies.

Our analysis shows that PWPs fall into five categories: theoretical, value conversion, value comparison, unknowns finding, and value change problems.

To convert problem text into the internal problem representation, we chose named entity recognition based on pattern matching. Other techniques for NER besides pattern matching on tokens can be used to analyze problem text, such as pattern matching on trees and statistical and neural models. Problem types are recognized based on the presence of particular entities. While this approach was sufficient on our small dataset, we have noticed that this solution could be easily broken. After NER, another step is required to convert a list of entities into the representation.

We have found a new kind of ambiguity: “quantity without a term”. This type of ambiguity occurs when the program finds a quantity entity that is a given value, but the program cannot infer the variable for this quantity. We partially solved this problem by inferring the variable by the unit of the quantity.

Our research shows that the algorithm for solving problems with unknown values is the STRIPS algorithm. Value change problems are complex problems to solve because of many non-trivial parameters. We hypothesize that these problems cannot be solved efficiently and belong to the class of “NP-hard” problems.

While our program can solve static computational physics problems, it is obvious that there are many other types of physics problems. Our program can be improved by choosing different NLP methods and by developing a more sophisticated problem representation.

REFERENCES